怎么算函数的周期_韦沟侔同学数学作业《怎么算函数的周期》解题方法_数学_韦沟侔
编辑: admin 2017-25-06
-
4
怎么算函数的周期导读:
这道数学作业题来自韦沟侔同学的作业解题方法分享《怎么算函数的周期》,指导老师是车老师,涉及到的数学知识点概括为:教下周期函数怎么算,同学们可以通过学习怎么算函数的周期:教下周期函数怎么算的相关数学知识来提升自己的数学作业解题能力,只有掌握了这些数学知识能力,才能让自己的数学解题能力提升,也才会在数学考试中取得良好的成绩,下面是韦沟侔数学作业的详细总结概括分享(本道题以问答模式展开)。
题目:教下周期函数怎么算
怎么算函数的周期:逆火学习站的韦沟侔同学的作业题:《教下周期函数怎么算》解题思路
定义通俗定义 对于函数y=f(x),如果存在一个不为零的常数T,使得当x取定义域内的每一个值时,f(x+T)=f(x)都成立,那么就把函数y=f(x)叫做周期函数,不为零的常数T叫做这个函数的周期. 严格定义 设f(x)是定义在数集M上的函数,如果存在非零常数T具有性质; (1)对 有(X±T) ; (2)对 有f(X+T)=f(X) 则称f(X)是数集M上的周期函数,常数T称为f(X)的一个周期.如果在所有正周期中有一个最小的,则称它是函数f(X)的最小正周期. 由定义可得:周期函数f(X)的周期T是与X无关的非零常数,且周期函数不一定有最小正周期. [编辑本段]周期函数性质 (1)若T(≠0)是f(X)的周期,则-T也是f(X)的周期. (2)若T(≠0)是f(X)的周期,则nT(n为任意非零整数)也是f(X)的周期. (3)若T1与T2都是f(X)的周期,则T1±T2也是f(X)的周期. (4)若f(X)有最小正周期T*,那么f(X)的任何正周期T一定是T*的正整数倍. (5)T*是f(X)的最小正周期,且T1、T2分别是f(X)的两个周期,则 (Q是有理数集) (6)若T1、T2是f(X)的两个周期,且T1/T2是无理数,则f(X)不存在最小正周期. (7)周期函数f(X)的定义域M必定是双方无界的集合. [编辑本段]周期函数的判定 定理1 若f(X)是在集M上以T*为最小正周期的周期函数则K f(X)+C(K≠0)和1/ f(X)分别是集M和集{X/ f(X) ≠0,X }上的以T*为最小正周期的周期函数. [1] 证: ∵T*是f(X)的周期,∴对 有X±T* 且f(X+T*)= f(X),∴K f(X)+C=K f(X+T*)+C, ∴K f(X)+C也是M上以T*为周期的周期函数. 假设T* 不是Kf(X)+C的最小正周期,则必存在T’( 0<T’<T*)是K f(X)+C的周期,则对 , 有K f(X+T’)+C=K f(X) +C K[f(X+T’)- f(X)]=0,∵K≠0,∴f(X+T’)- f(X)=0,∴f(X+T’)= f(X), ∴T’是f(X)的周期,与T*是f(X)的最小正周期矛盾,∴T*也是K f(X)+C的最小正周期. 同理可证1/ f(X)是集{X/ f(X) ≠0,X }上的以T*为最小正周期的周期函数. 定理2 若f(X)是集M上以T*为最小正周期的周期函数,则f(aX+n)是集{X/aX+ b }上的以T*/ 为最小正周期的周期函数,(其中a、b为常数). 证: 先证 是f(ax+b)的周期 ∵T*是f(X)的周期,∴ ,有X±T*∈M,∴a(X± )+b=ax+b±T*∈M,且f[a(X+ )+b]=f(ax+b±T*)=f(ax+b)∴ 是f(ax+b)的周期. 再证 是f(ax+b)的最小正周期 假设存在T’(0<T’< )是f(ax+b)的周期, 则f(a(x+T’)+b)=f(ax+b),即f(ax+b+aT’)=f(ax+b), 因当X取遍{X/X∈M,ax+b∈M}的各数时,ax+b就取遍M所有的各数, ∴aT’是f(X)的周期,但 <=T*这与T*是f(X)的最小正周期矛盾. 定理3 设f(u)是定义在集M上的函数u=g(x)是集M1上的周期函数,且当X∈M1时,g(x)∈M,则复合函数f(g(x))是M1上的周期函数. 证: 设T是u=g(x)的周期,则 1有(x±T)∈M1且g(x+T)=g(x) ∴f(g(x+T))=f(g(x)) ∴=f(g(x))是M1上的周期函数. 例1 设=f(u)=u2是非周期函数,u= g(X)=cosx是实数集R上的周期函数,则f(g(x))=cos2x是R上的周期函数. 同理可得:(1)f(X)=Sin(cosx),(2)f(X)=Sin(tgx),(3)f(X)=Sin2x,(4)f(n)=Log2Sinx(sinx>0)也都是周期函数. 例2 f(n)=Sinn是周期函数,n=g(x)=ax+b(a≠0)是非周期函数,f(g(x))=Sin(ax+b)是周期函数(中学数学中已证). 例3 f(n)=cosn是周期函数,n=g(x)= (非周期函数)而f(g(x))=cos 是非周期函数. 证:假设cos 是周期函数,则存在T>0使cos (k∈Z) 与定义中T是与X无关的常数矛盾, ∴cos 不是周期函数. 由例2、例3说明,若f(u)是周期函数,u= g(X)是非周期函数,这时f(g(x))可能是,也可能不是周期函数. 定理4 设f1(X)、f2(X)都是集合M上的周期函数,T1、T2分别是它们的周期,若T1/T2∈Q则它们的和差与积也是M上的周期函数,T1与T2的公倍 数为它们的周期. 证: 设 ((p·q)=1)设T=T1q=T2p则有: 有(x±T)=(x±T1q)=(x±T2p)∈M,且f1(x+T) ±f2(x+T)= f1(x+T1q) ±f2(x+T2p)= f1(X)±f2(X) ∴f1(X) ±f2(X)是以T1和T2的公倍数T为周期的周期函数.同理可证:f1(X) 、f2(X)是以T为周期的周期函数. 定理4推论 设f1(X) 、f2(X)……fn(X) 是集M上的有限个周期函数T1、T2……Tn分别是它们的周期,若, … (或T1,T2……Tn中任意两个之比)都是有理数,则此n个函数之和、差、积也是M上的周期函数. 例4 f(X)=Sinx-2cos2x+sin4x是以2π、π、π/2的最小公倍 数2π为周期的周期函数. 例5 讨论f(X)= 的周期性 2tg3 是以T1= 为最小正周期的周期函数. 5tg 是以T2 为最小正周期的周期函数. tg2 是以T3= 为最小正周期的周期函数. 又 都是有理数 ∴f(X)是以T1、T2、T3最小公倍数(T1、T2、T3)= 为最小正周期的周期函数. 同理可证: (1)f(X)=cos ; (2)f(x)=sin2xcos2x+cos2xcos3x+cos3xsin3x.是周期函数. 定理5 设f1(x)=sin a1x,f2(x)=cosa2x,则f1(x)与f2(x)之和、差、积是周期函数的充要条件是a1/a2∈Q. 证 先证充分性: 若a1/a2∈Q,设T1、T2分别为f1(x)与f2(x)的最小正周期,则T1= 、T2= ,又 ∈Q 由定理4可得f1(x)与f2(x)之和、差、积是周期函数. 再证必要性(仅就f1(x)与f2(x)的差和积加以证明). (1)设sina1x-cosa2x为周期函数,则必存在常数T>0, 使sina1(x+T)-sina1x=cosa2(x+T)-cosa2x 2cos(a1x+ )sin = -2sin s(a2x+ ) sin (1). 令x= 得2cos(a1x+ ),则 (K∈Z).(2) 或 C∈Z(3) 又在(1)中令 2sin(a2x+ )sin =-2sin =0 由(4) 由sin (5) 由上述(2)与(3),(4)与(5)都分别至少有一个成立. 由(3)、(5得 )(6) ∴无论(2)、(4)、(6)中那一式成立都有a1/a2 . (2)设sinaxcosa2x为周期函数,则 是周期函数. [编辑本段]非周期函数的判定 [1](1)若f(X)的定义域有界 例:f(X)=cosx( ≤10)不是周期函数. (2)根据定义讨论函数的周期性可知非零实数T在关系式f(X+T)= f(X)中是与X无关的,故讨论时可通过解关于T的方程f(X+T)- f(X)=0,若能解出与X无关的非零常数T便可断定函数f(X)是周期函数,若这样的T不存在则f(X)为非周期函数. 例:f(X)=cos 是非周期函数. (3)一般用反证法证明.(若f(X)是周期函数,推出矛盾,从而得出f(X)是非周期函数). 例:证f(X)=ax+b(a≠0)是非周期函数. 证:假设f(X)=ax+b是周期函数,则存在T(≠0),使对 ,a(x+T)+b=ax+b ax+aT-ax=0 aT=0 又a≠0,∴T=0与T≠0矛盾,∴f(X)是非周期函数. 例:证f(X)= 是非周期函数. 证:假设f(X)是周期函数,则必存在T(≠0)对 ,有(x+T)= f(X),当x=0时,f(X)=0,但x+T≠0, ∴f(x+T)=1,∴f(x+T) ≠f(X)与f(x+T)= f(X)矛盾,∴f(X)是非周期函数. 例:证f(X)=sinx2是非周期函数 证:若f(X)= sinx2是周期函数,则存在T(>0),使对 ,有sin(x+T)2=sinx2,取x=0有sinT2=sin0=0,∴T2=Kπ(K∈Z),又取X= T有sin( T+T)2=sin( T)2=sin2kπ=0,∴( +1)2 T2=Lπ(L∈Z+),∴ 与3+2 是无理数矛盾,∴f(X)=sinx2是非周期函数.互助这道作业题的同学还参与了下面的作业题
题1: 【第五题函数周期怎么算】[数学科目]
4sin^3(x)cosx = 2sin^2(x) * 2sinxcosx = (1-cos2x) * sin2x = sin2x - sin2xcos2x = sin2x - (1/2)sin4x所以f(x) = (1/2)sin4x怎么算函数的周期:逆火学习站的韦沟侔同学的作业题:《教下周期函数怎么算》解题思路
其最小正周期是pi/2,选C题2: 【这个函数的最小周期怎么算?】[数学科目]
怎么算函数的周期:逆火学习站的韦沟侔同学的作业题:《教下周期函数怎么算》解题思路
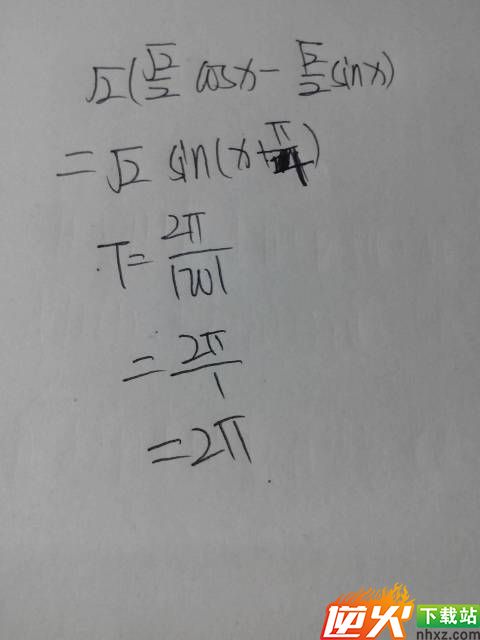
题3: 请问2个周期函数的和函数、积函数的周期怎么算?[数学科目]
两个周期函数和的周期通常是先求两个函数的最小正周期,再求它们的最小公倍数,即为和函数的最小正周期;怎么算函数的周期:逆火学习站的韦沟侔同学的作业题:《教下周期函数怎么算》解题思路
两个周期函数的积的周期没有一定的结论,通常是根据式子的特点,经过运算,结合周期函数的定义求出积的周期.另外,和函数的周期有时候不可公度,即不存在最小公倍数.题4: 函数最小正周期怎么算[数学科目]
只要证明f(x+T)=f(x)在函数的定义域内恒成立,且T是最小的能怎么算函数的周期:逆火学习站的韦沟侔同学的作业题:《教下周期函数怎么算》解题思路
保证f(x+T)=f(x)成立,则函数的函数最小正周期为T.题5: 怎么算这个函数的周期f=5*sin(2*pi*20*t)+5*sin(2*pi*60*t);不太会求,因为题目涉及到球采样频率的范围,所以可能会用到信号与系统的知识,[数学科目]
这个其实只要求出两个函数的最小正周期取最小公倍数就行了第一个T1=2π/(40π)=1/20第二个T2=2π/(120π)=1/60怎么算函数的周期:逆火学习站(img1.72589.com)的韦沟侔同学的作业题:《教下周期函数怎么算》解题思路
怎么算函数的周期小结:
通过以上关于韦沟侔同学对怎么算函数的周期:教下周期函数怎么算的概括总结详细分享,相信同学们已经对怎么算函数的周期的相关数学作业知识一定有所收获吧。建议同学们要学会归纳总结,仔细揣摩韦沟侔同学分享的解答《教下周期函数怎么算》这道作业题的重点部分,他山之石,可以攻玉,考才获胜。
