如图a是y轴正半轴_石侍下同学数学作业《如图a是y轴正半轴》解题方法_数学_石侍下
编辑: admin 2017-25-06
-
4
如图a是y轴正半轴导读:
这道数学作业题来自石侍下同学的作业解题方法分享《如图a是y轴正半轴》,指导老师是吕老师,涉及到的数学知识点概括为:如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45...,同学们可以通过学习如图a是y轴正半轴:如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45...的相关数学知识来提升自己的数学作业解题能力,只有掌握了这些数学知识能力,才能让自己的数学解题能力提升,也才会在数学考试中取得良好的成绩,下面是石侍下数学作业的详细总结概括分享(本道题以问答模式展开)。
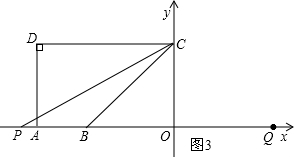
题目:如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45...
如图a是y轴正半轴:逆火学习站的石侍下同学的作业题:《如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45...》解题思路
(1)∵∠BCO=∠CBO=45°, ∴OC=OB=3,
∴OC=OB=3,又∵点C在y轴的正半轴上,
∴点C的坐标为(0,3);
(2)分两种情况考虑:
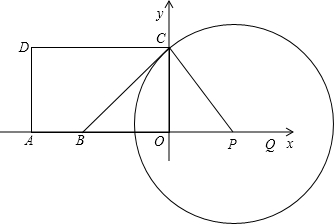
①当点P在点B右侧时,如图2,
若∠BCP=15°,得∠PCO=30°,
 故PO=CO?tan30°=
故PO=CO?tan30°=| 3 |
| 3 |
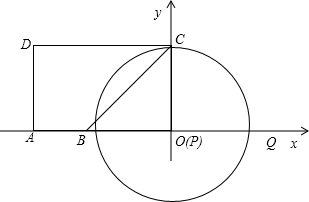
②当点P在点B左侧时,如图3,
由∠BCP=15°,得∠PCO=60°,
故OP=COtan60°=3
| 3 |
此时,t=4+3
| 3 |
∴t的值为4+
| 3 |
| 3 |
(3)由题意知,若⊙P与四边形ABCD的边相切时,有以下三种情况:
①当⊙P与BC相切于点C时,有∠BCP=90°,
从而∠OCP=45°,得到OP=3,此时t=1;
②当⊙P与CD相切于点C时,有PC⊥CD,即点P与点O重合,此时t=4;
③当⊙P与AD相切时,由题意,得∠DAO=90°,
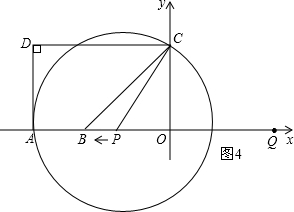
∴点A为切点,如图4,PC2=PA2=(9-t)2,PO2=(t-4)2,
于是(9-t)2=(t-4)2+32,即81-18t+t2=t2-8t+16+9,
解得:t=5.6,
∴t的值为1或4或5.6.
互助这道作业题的同学还参与了下面的作业题
题1: 如图ab两点的坐标分别为(-5,0)(-3.0),点c在y轴的正半轴上,角cbd=45度,cd平行ab,cda=90度点p从点q(4,0)出发,延x轴向左以每秒1个单位长度的速度运动,运动时间有t秒.(1)求点c的坐标(2)当[数学科目]
(1)∵∠BCO=∠CBO=45°,∴OC=OB=3,又∵点C在y轴的正半轴上,∴点C的坐标为(0,3); (2)分两种情况考虑:①当点P在点B右侧时,如图2,若∠BCP=15°,得∠PCO=30°,故PO=CO•tan30°=,此时t=4+; ②当点P在点B左侧时,如图3,由∠BCP=15°,得∠PCO=60°,故OP=COtan60°=3,此时,t=4+3,∴t的值为4+或4+3; (3)由题意知,若⊙P与四边形ABCD的边相切时,有以下三种情况:①当⊙P与BC相切于点C时,有∠BCP=90°,从而∠OCP=45°,得到OP=3,此时t=1; ②当⊙P与CD相切于点C时,有PC⊥CD,即点P与点O重合,此时t=4; ③当⊙P与AD相切时,由题意,得∠DAO=90°,∴点A为切点,如图4,PC2=PA2=(9﹣t)2,PO2=(t﹣4)2,于是(9﹣t)2=(t﹣4)2+32,即81﹣18t+t2=t2﹣8t+16+9,解得:t=5.6,如图a是y轴正半轴:逆火学习站的石侍下同学的作业题:《如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45...》解题思路
∴t的值为1或4或5.6.题2: 如图,AB是圆O的直径,点C在AB的延长线上,CD与圆O相切于点D若角C等于18度,则角CDA?[数学科目]
连接OD.CD与圆O切于D,则OD垂直CD,∠COD=90°-∠C=72°.∵OD=OA.∴∠ADO=∠DAO=(1/2)∠COD=36°.如图a是y轴正半轴:逆火学习站的石侍下同学的作业题:《如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45...》解题思路
所以,∠CDA=∠ADO+∠CDO=126° .题3: 如图,二次函数y=ax²+2ax+4的图像与X轴交于A、B,与Y轴交C,∠CBO的正切值是2[1]求此二次函数的解析式[2]动直线l从直线AC重合的位置出发,绕点A顺时针旋转,与直线AB重合时中止运动,直线l与BC交于[数学科目]
二次函数y=ax²+2ax+4的图像与X轴交于A、B,与Y轴交C,∠CBO的正切值是2;[1]求此二次函数的解析式tan∠CBO=∣OC∣/∣OB∣=4/∣OB∣=2,故OB=4/2=2;即B(2,0);将B点的坐标代入抛物线方程得4a+4a+4=8a+4=0,故a=-1/2...题4: 如图,角CDA与角CBD等于90度,点E,F分别是线段CD,AB的中点,求证EF垂直AB
【只有∠CAD=∠CBD=90°时,EF⊥AB】证明:连接AE,BE∵∠CAD=90°,E是CD的中点∴AE=½CD(直角三角形斜边中线等于斜边的一半)∵∠CBD=90°,E是CD的中点∴BE=½CD∴AE=BE∵F是AB的中点如图a是y轴正半轴:逆火学习站的石侍下同学的作业题:《如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45...》解题思路
∴EF⊥AB(等腰三角形三线合一)题5: 【A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD〃AB,∠CDA=45°,点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时间为t秒.(1),求点C的坐标,(2),以点P为圆心,PC为半经的⊙P随点P的运动】[数学科目]
(1)∵∠BCO=∠CBO=45°,∴OC=OB=3,又∵点C在y轴的正半轴上,∴点C的坐标为(0,3);(2)分两种情况考虑:①当点P在点B右侧时,如图2,若∠BCP=15°,得∠PCO=30°,故PO=CO•tan30°= 3 ,此时t=4+ 3 ;②当点P在点B左侧时,如图3,由∠BCP=15°,得∠PCO=60°,故OP=CO×tan60°=3 3 ,此时,t=4+3 3 ,∴t的值为4+ 3 或4+3 3 ;(3)由题意知,若⊙P与四边形ABCD的边相切时,有以下三种情况:①当⊙P与BC相切于点C时,有∠BCP=90°,从而∠OCP=45°,得到OP=3,此时t=1;②当⊙P与CD相切于点C时,有PC⊥CD,即点P与点O重合,此时t=4;③当⊙P与AD相切时,由题意,得∠DAO=90°,∴点A为切点,如图4,PC2=PA2=(9-t)2,PO2=(t-4)2,于是(9-t)2=(t-4)2+32,即81-18t+t2=t2-8t+16+9,解得:t=5.6,如图a是y轴正半轴:逆火学习站(img1.72589.com)的石侍下同学的作业题:《如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45...》解题思路
如图a是y轴正半轴小结:
通过以上关于石侍下同学对如图a是y轴正半轴:如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45...的概括总结详细分享,相信同学们已经对如图a是y轴正半轴的相关数学作业知识一定有所收获吧。建议同学们要学会归纳总结,仔细揣摩石侍下同学分享的解答《如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45...》这道作业题的重点部分,他山之石,可以攻玉,考才获胜。
