如图1在边长为4_沈纸蜒同学数学作业《如图1在边长为4》解题方法_数学_沈纸蜒
编辑： admin 2017-25-06
-
4
如图1在边长为4导读：
这道数学作业题来自沈纸蜒同学的作业解题方法分享《如图1在边长为4》，指导老师是寿老师，涉及到的数学知识点概括为：如图1点pq分别是边长为4厘米等边三角形abc，同学们可以通过学习如图1在边长为4：如图1点pq分别是边长为4厘米等边三角形abc的相关数学知识来提升自己的数学作业解题能力，只有掌握了这些数学知识能力，才能让自己的数学解题能力提升，也才会在数学考试中取得良好的成绩，下面是沈纸蜒数学作业的详细总结概括分享（本道题以问答模式展开）。
题目：如图1点pq分别是边长为4厘米等边三角形abc
（1）∠CMQ=60°不变．∵等边三角形中,AB=AC,∠B=∠CAP=60°又由条件得AP=BQ,∴△ABQ≌△CAP（SAS）,∴∠BAQ=∠ACP,∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°．（2）设时间为t,则AP=BQ=t,PB=4-t①当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,得4-t=2t,t=43；②当∠BPQ=90°时,∵∠B=60°,∴BQ=2BP,得t=2（4-t）,t=83；∴当第43秒或第83秒时,△PBQ为直角三角形．（3）∠CMQ=120°不变．∵在等边三角形中,AB=AC,∠B=∠CAP=60°∴∠PBC=∠ACQ=120°,又由条件得BP=CQ,∴△PBC≌△QCA（SAS）∴∠BPC=∠MQC又∵∠PCB=∠MCQ,如图1在边长为4：逆火学习站的沈纸蜒同学的作业题：《如图1点pq分别是边长为4厘米等边三角形abc》解题思路
∴∠CMQ=∠PBC=180°-60°=120°互助这道作业题的同学还参与了下面的作业题
题1： 【如图,一个边长是1厘米的等边三角形ABC,将它沿直线L作顺时针方向的翻动,到达图中最右边三角形的位置,试在A、B、C三个顶点中选一个点,求该点所经过的路程是多少厘米?（精确到0.01厘米）】[数学科目]
是练习册上的吧!C=2πr=2×3.14×1=6.28×1如图1在边长为4：逆火学习站的沈纸蜒同学的作业题：《如图1点pq分别是边长为4厘米等边三角形abc》解题思路
=6.28题2： 【如图,在边长为6的正三角形△ABC中,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值和最小值】[数学科目]
利用平行四边形两邻边平方和等于其对角线平方和的一半也等于对角线一半的平方和的二倍,后附证明见图2△APQ三边平方和=AP²+AQ²+PQ²,其中PQ²=4如图1在边长为4：逆火学习站的沈纸蜒同学的作业题：《如图1点pq分别是边长为4厘米等边三角形abc》解题思路
如果以AP,AQ为邻边做平行四边形APDQ,则PQ是这个平行四边形的一条对角线,另外一条对角线是AD的中点O在BC边上,同时AO也是△APQ的中线,由于平行四边形两邻边平方和等于对角线平方和的一半AP²+AQ²=(PQ²+AD²)/2=2(PO²+AO²) PO=PQ/2=1所以△APQ三边平方和=2(PO²+AO²)+PQ²=2PO²+PQ²+2AO²=6+2AO²随着P,Q两点在BC边上滑动,AO的长度随着变化,AO最短的时候为ABC底边上的高=3根号3最长的时候为P点和B点重合的时候（Q点和C点重合也是一样的）,这个时候BO=1,AO=根号31所以△APQ三边平方和最大=6+2×31=68,最小=6+2×27=60证明：平行四边形两邻边平方和等于对角线平方和,参考图1RT△ABH中,AB²=AH²+BH²RT△BCH中,BC²=BH²+CH²RT△BOH中,BH²=BO²-OH²AH=AO-OH CH=CO+OH AO=COAH²+CH²=(AO-OH)²+(CO+OH)²=AO²+CO²+2OH²如图1在边长为4：逆火学习站的沈纸蜒同学的作业题：《如图1点pq分别是边长为4厘米等边三角形abc》解题思路
AB²+BC²=AH²+CH²+2BH²=AO²+CO²+2OH²+2(BO²-OH²)=2(AO²+BO²)=(AC²+BD²)/2AO和BO是对角线的一半如图1在边长为4：逆火学习站的沈纸蜒同学的作业题：《如图1点pq分别是边长为4厘米等边三角形abc》解题思路
题3： 如图△ABC是等边三角形,AE=CD,AD,BE相交于点P.BQ垂直于AD于Q,PQ=3,PE=1.求AD的长图：[数学科目]
∵△ABC 是等边三角形∴∠BAE=∠C=60°∵AB=AC,AE=CD∴ABE≌△CAD∴∠CAD=∠ABE,BE=AD∴∠BPD=∠PAB+∠ABE=∠PAB+∠CAD=60°∵BQ⊥AQ∴∠PBQ=30°∴BP=2PQ=6∴BE=BP+PE=6+1=7如图1在边长为4：逆火学习站的沈纸蜒同学的作业题：《如图1点pq分别是边长为4厘米等边三角形abc》解题思路
∴AD=7题4： 如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，则DE的长为（）A.13B.12C.23D.不能确定[数学科目]
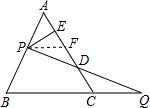过P作PF∥BC交AC于F．∵PF∥BC，△ABC是等边三角形，
∴∠PFD=∠QCD，△APF是等边三角形，
∴AP=PF=AF，
∵PE⊥AC，
∴AE=EF，
∵AP=PF，AP=CQ，
∴PF=CQ．
∵在△PFD和△QCD中，
|
∴△PFD≌△QCD（AAS），
∴FD=CD，
∵AE=EF，
∴EF+FD=AE+CD，
∴AE+CD=DE=
| 1 |
| 2 |
∵AC=1，
∴DE=
| 1 |
| 2 |
故选B．
题5： 如图,在三角形ABC中,角ACB=90度,AC=BC,过C点任做一直线PQ,AM垂直于PQ于M,BN垂直于PQ于N,求证,MN=AM+BN[数学科目]
证：∵∠ACB=90°∴∠BCN+∠ACM=90°又∵∠CAM+∠ACM=90°∴∠BCN=∠CAM又∵BC=AC∴Rt△BCN≌△CAM∴CN=AM ,CM=BN∴CN+CM=AM+BN如图1在边长为4：逆火学习站(img1.72589.com)的沈纸蜒同学的作业题：《如图1点pq分别是边长为4厘米等边三角形abc》解题思路
如图1在边长为4小结：
通过以上关于沈纸蜒同学对如图1在边长为4：如图1点pq分别是边长为4厘米等边三角形abc的概括总结详细分享，相信同学们已经对如图1在边长为4的相关数学作业知识一定有所收获吧。建议同学们要学会归纳总结，仔细揣摩沈纸蜒同学分享的解答《如图1点pq分别是边长为4厘米等边三角形abc》这道作业题的重点部分，他山之石，可以攻玉，考才获胜。