1×n矩阵的逆矩阵_扶惹罕同学数学作业《1×n矩阵的逆矩阵》解题方法_数学_扶惹罕
编辑: admin 2017-25-06
-
4
1×n矩阵的逆矩阵导读:
这道数学作业题来自扶惹罕同学的作业解题方法分享《1×n矩阵的逆矩阵》,指导老师是蓝老师,涉及到的数学知识点概括为:这个上三角全为1的n×n矩阵的逆是什么?,同学们可以通过学习1×n矩阵的逆矩阵:这个上三角全为1的n×n矩阵的逆是什么?的相关数学知识来提升自己的数学作业解题能力,只有掌握了这些数学知识能力,才能让自己的数学解题能力提升,也才会在数学考试中取得良好的成绩,下面是扶惹罕数学作业的详细总结概括分享(本道题以问答模式展开)。
题目:这个上三角全为1的n×n矩阵的逆是什么?
逆矩阵如下图,可用(A,E)作行初等变换方法求得.经济数学团队帮你解答,请及时采纳.1×n矩阵的逆矩阵:逆火学习站的扶惹罕同学的作业题:《这个上三角全为1的n×n矩阵的逆是什么?》解题思路
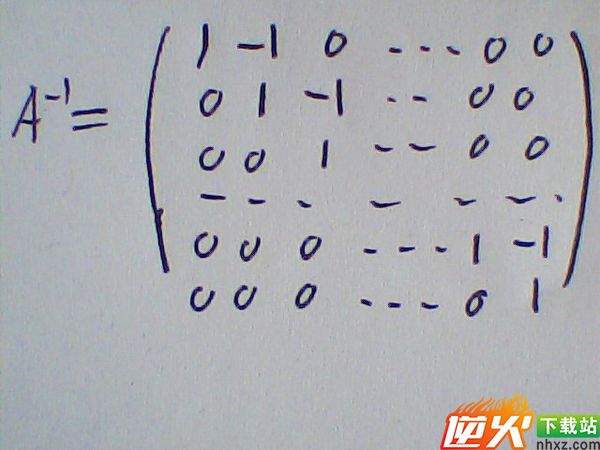
互助这道作业题的同学还参与了下面的作业题
题1: 任何n阶矩阵是一组三角矩阵(包括上三角矩阵和下三角矩阵)的乘积希望能详细说明,偶滴线代基础太差了%>_忘了说,这是一道证明题[数学科目]
前提是你得知道矩阵通过一系列 (有限步) 行初等变换可以转化到阶梯型,而对于方阵而言阶梯型一定是上三角阵,所以只要证明那一系列行变换都是三角矩阵就行了.第二类初等变换是对角阵,第三类初等变换是三角矩阵,唯有第一类变换需要验证1×n矩阵的逆矩阵:逆火学习站的扶惹罕同学的作业题:《这个上三角全为1的n×n矩阵的逆是什么?》解题思路
事实上第一类初等变换可以用另外两类变换来表示,见题2: 请问n阶上三角矩阵的维数为什么是n*(n+1)/2呢?[数学科目]
第i列有i个自由度,所以维数就是1+2+...+n=n(n+1)/21×n矩阵的逆矩阵:逆火学习站的扶惹罕同学的作业题:《这个上三角全为1的n×n矩阵的逆是什么?》解题思路
正式一点讲,恰好有一个元素为1,其余元素为0的上三角矩阵构成空间的一组基,这样的矩阵有n(n+1)/2个题3: 读入一个正整数n(1≤n≤6),再读入n阶矩阵a,计算上三角的和.
#include void main(){int n;int a[6][6];int i,j,sum=0;printf("input n ");scanf("%d",&n);printf("input n*n matrix ");1×n矩阵的逆矩阵:逆火学习站的扶惹罕同学的作业题:《这个上三角全为1的n×n矩阵的逆是什么?》解题思路
for (j=0;j题4: 定义一个N*N的矩阵,输出其对角线元素、上三角矩阵和下三角矩阵;要考试急
要用什么实现matlab 有函数diag1×n矩阵的逆矩阵:逆火学习站的扶惹罕同学的作业题:《这个上三角全为1的n×n矩阵的逆是什么?》解题思路
A=rand(3,3);B=diag(A);C=tril(A);D=triu(A)题5: 请问一下三角矩阵是上三角矩阵还是下三角矩阵?0001002003004000不好意思,我想问的是在编程中输入以下的矩阵是算上三角,还是下三角,或两个都不是。(只有上(下)三角之分
0 0 0 1 0 0 2 0 0 3 0 0 4 0 0 0这是斜对角1 0 0 1 0 0 2 0 0 3 0 0 4 0 0 0这是斜上三角.对应也有斜下三角1×n矩阵的逆矩阵:逆火学习站(img1.72589.com)的扶惹罕同学的作业题:《这个上三角全为1的n×n矩阵的逆是什么?》解题思路
1×n矩阵的逆矩阵小结:
通过以上关于扶惹罕同学对1×n矩阵的逆矩阵:这个上三角全为1的n×n矩阵的逆是什么?的概括总结详细分享,相信同学们已经对1×n矩阵的逆矩阵的相关数学作业知识一定有所收获吧。建议同学们要学会归纳总结,仔细揣摩扶惹罕同学分享的解答《这个上三角全为1的n×n矩阵的逆是什么?》这道作业题的重点部分,他山之石,可以攻玉,考才获胜。
