特征多项式_师偶傲同学的作业《特征多项式》各个击破_其他_师偶傲
编辑: admin 2017-25-06
-
要理解特征多项式,首先需要了解一下特征值与特征向量,这些都是联系在一起的: 设A是n阶矩阵,如果数λ和数n为非零列向量x使得关系式 Ax=λx 成立,那么,这样的数λ就称为方阵A的特征值,非零向量x称为A对应于特征值λ的特征向量。 然后,我们也就可以对关系式进行变换: (A-λE)x=0 其中E为单位矩阵 这是n个未知数n个方程的齐次线性方程组,它有非零解的充要条件是系数行...
互助这道作业题的同学还参与了下面的作业题
题1: 什么是特征多项式是高等代数的哪一章的哪一点的知识?快[数学科目]
矩阵A的特征多项式为|λE-A|.对于你的这道题,矩阵A的特征多项式为|λE-A|= | λ+1 -1 0 | | 4 λ-3 0 |=(λ-2)[(λ+1)(λ-3)+4]=(λ-2)(λ^2-2λ+1)=λ^3-4λ^2+5λ-2特征多项式:逆火学习站的师偶傲同学的作业题:《关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...》解题思路
| -1 0 λ-2|题2: 特征多项式问题A的特征值a1,a2,特征多项式p1,p2则A^2-2A+3E+2A^-1的特征多项式是?[数学科目]
A的特征值a1,a2,特征多项式p1,p2则A^2-2A+3E+2A^-1的特征多项式是?打印错误!应该是A的特征值a1,a2,对应的特征向量p1,p2则A^2-2A+3E+2A^-1的特征值与对应的特征向量是什么?∵出现2A^-1,∴a1,a2都不为零.A^2-2A+3E+2A^-1的特征值为a1²-2a1+3+2/a1,a2²-2a2+3+2/a2,特征多项式:逆火学习站的师偶傲同学的作业题:《关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...》解题思路
对应的特征向量还是p1,p2.题3: 矩阵A的特征多项式怎么求出来的.|λ-320||λI-A|=|1λ-31|=(λ-2)^2(λ-1)|5-7λ+1|我想知道,后面这个因式是怎么的出来的.[数学科目]
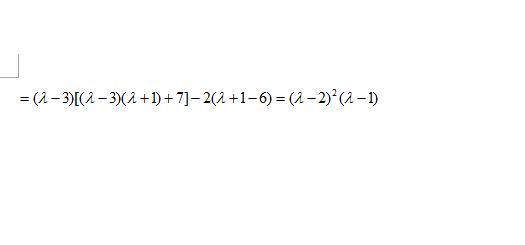
题4: 关于特征多项式这是课本上的一段原文我的想法是,不用这么复杂,直接代入,即特征多项式=|A-λE|=|A-AE|=O不知道对不对,请高手指点!这是原文:我给丢了,SORRYhttp://hi.baidu.com/lovesophialove/blog/[数学科目]
你的做法是错误的!你注意f(A)计算出来的结果应该是一个矩阵,即应该是与A同型号的O矩阵.而按你那样算的话结果出来就是数字0了,所以你的计算显然是错的.特征多项式:逆火学习站(img1.72589.com)的师偶傲同学的作业题:《关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...》解题思路
特征多项式小结:
通过以上关于师偶傲同学对特征多项式:关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...的解题笔记分享,相信同学们已经对特征多项式的相关作业考点会有所突破。只有平时多努力,才会有好的成绩,相信通过师偶傲同学分享的解答《关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...》的这道作业题不断的各个击破才会突破自我。
-
4
特征多项式导读:
本道作业题是师偶傲同学分享给同学们的课后拓展作业题目。主要是围绕特征多项式知识进行展开问答,目的是各个击破,考核的主要知识点是——《特征多项式:关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...》,指导老师是戎老师,可能与教科书相关的知识点为:关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...,主要考察特征多项式:关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...的相关知识考点,下面是师偶傲的对这道作业的问答方式进行的分享(本道题以问答模式展开)。
题目:关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...
这个不是推导出来的,是分两步来的:首先证明|λE-A|是一个多项式,最高项是n次的.这只需要按照行列式的定义就行了.第二步,证明各次的前边系数有你给的那个规律.特征多项式:逆火学习站的师偶傲同学的作业题:《关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...》解题思路
我们知道n次多项式在复数域内一定有n个根,这是复数基本定理.那么|λE-A|这个n次多项式在复数域内一定可以因式分解成n个因子的乘积形式|λE-A|=(λ-λ1)(λ-λ2).(λ-λn),其中λ1.λn就叫特征多项式的特征值.把这个多项式|λE-A|=(λ-λ1)(λ-λ2).(λ-λn),和你给的系数正好对应相等.特征多项式:逆火学习站的师偶傲同学的作业题:《关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...》解题思路
例如,常数项为(-1)^n|A|,而|A|正是λ1λ2.λn,又例如n-1次项 - (a11 + a22 + … + ann),而由于相似矩阵对迹tra的相似不变性这个正好等于 - (λ1 + λ2 + … + λn).综上第一步是按照行列式定义成多项式形式,发现他是n次多项式(系数是什么还不清楚).第二步根据代数基本定理写成因式分解形式|λE-A|=(λ-λ1)(λ-λ2).(λ-λn)再,然后根据特征值具有的性质证明你给的式子正确.特征多项式:逆火学习站的师偶傲同学的作业题:《关于特征多项式?λE-A = λ^n - (a11 + a22 + … +...》解题思路
落下了点东西,第一步还要说明最高项次数为1(首一),因为矩阵中含有λ的元素都在对角线上,按照按行按列(行列式的拉普拉斯)只有对角线乘积这一个是λ的n次的,其余项都比他次数小,所以最高项一定是λ^n无他