【已知直线ab过点a】已知直线AB经过点A(0，5)，B(2，0)，若将这条直线向左平..._数学_罪恶王冠5gN
编辑： admin 2017-15-06
-
4
可设原直线解析式为y=kx+b，则点A（0，5），B（2，0）适合这个解析式，
则b=5，2k+b=0．解得k=-2.5．
平移不改变k的值，∴y=-52
互助这道作业题的同学还参与了下面的作业题
题1： 已知直线AB经过点A（0,5）,B（2,0）,若将这条直线向左平移,恰好过坐标原点,则平移后的直线解析式
直线AB经过点A（0,5）,B（2,0）
AB：y=-2.5x+5
若将这条直线AB向左平移,恰好过坐标原点
k不变,仍为-2.5
平移后的直线解析式：y=-2.5x
题2： 在平面直角坐标系中，已知点A（-4，0）、B（0，2），现将线段AB向右平移，使A与坐标原点O重合，则B平移后的坐标是______．[数学科目]
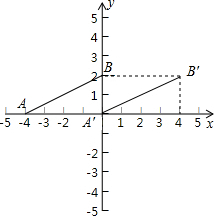如图，已知点A（-4，0）、B（0，2），
将线段AB向右平移，使A与坐标原点O重合，
∴点B的坐标是（4，2）；
故答案为（4，2）．
题3： 已知点A（2,-4）B（4,0）,连接AB,把AB所在直线沿y轴向上平移,使它经过原点O,得到直线L,设P是直线L上一个动点1.求直线AB的解析式2.设以点ABOP为顶点的四边形的面积为S,点P的横坐标为X,求S与X的函[数学科目]
1.设直线AB的解析式为y=kx+b,
把A,B的坐标代入得
2k+b=-4,
4k+b=0.
解得k=2,b=-8.
∴AB的解析式为y=2x-8.
2.L:y=2x.
P(x,2x).过P作PQ⊥x轴于Q,AC⊥x轴于C,则
x<0时点ABOP为顶点的四边形的面积为S
=S△ABC+S(梯形ACQP)-S△OPQ
=4+(4-2X)(2-X)/2-X^2
=8-4x;
x>0时点ABOP为顶点的四边形的面积为S
=S△ABO+S△PBO
=8+4x.
题4： 直线y=x向左平移t个单位(t>0),与交x轴与点A,交y轴与点B,坐标原点O关于直线AB的对称点M,点M恰好在反比例函数y=k/x的图像上.（1）当t=1时,求直线AB及反比例函数的解析式.（2）若作直线MO,交反比例[数学科目]
平移后的直线为：y=x+t,点A的坐标为（-t,0）,点B的坐标为（0,-t）
由于M是原点O关于直线的对称点,而△OAB是等腰直角三角形,∠AOB是直角,
故四边形OAMB是正方形,点M的坐标为（-t,t）
（1）当t=1时,直线AB的解析式为：y=x+1
M的坐标为（-1,1）,带入反比例函数y=k/x中得：k=-1,那么反比例函数的解析式为：y=-1/x
（2）直线MO交反比例函数于点N,则点N是点M关于点O的对称点,点N的坐标为（t,-t）
所以△OAN与△OBN的面积相等,都等于t^2/2,而正方形OAMB的面积为t^2
得到：t^2/2+t^2/2+t^2=8,解得：t=2,
M的坐标为（-2,2）,带入反比例函数y=k/x中得：k=-4,那么反比例函数的解析式为：y=-4/x
（3）t=3,得到k=-9,反比例函数的解析式为：y=-9/x,点P的坐标为（0,3*tan（a+45°））,
则点Q的坐标为（-3/tan（a+45°）,3*tan（a+45°））
设直线AM与直线PQ交于点C,
则四边形APQM的面积=四边形OACP的面积-△MCQ的面积-△OAP的面积,
设r=| tan（a+45°）|,则9*r-(3-3/r)(3*r-3)/2-9*r/2=9-3根号3/2,
解得：r=二分之根号六,故a+45°=60°或120°,
得：a=15°或75°
题5： 【如图，Rt△OAB中，∠OAB=90°，O为坐标原点，边OA在x轴上，OA=AB=1个单位长度，把Rt△OAB沿x轴正方向平移1个单位长度后得△AA1B1．（1）求以A为顶点，且经过点B1的抛物线的解析式；（2）若（1）】[数学科目]
（1）由题意可知，A（1，0），A1（2，0），B1（2，1），
设以A为顶点的抛物线的解析式为y=a（x-1）2；
∵此抛物线过点B1（2，1），
∴1=a（2-1）2，
∴a=1，
∴抛物线的解析式为y=（x-1）2；
（2）∵当x=0时，y=（0-1）2=1，
∴D点坐标为（0，1），
由题意得OB在第一象限的角平分线上，
故可设C（m，m），
代入y=（x-1）2；得m=（m-1）2；
解得m1=3?52＜1
故C点坐标为（3?52，3?52）．