【如图P在角A0B内部】已知角AOB=30度，点P在角A0B的内部，点P1与P关于OB对称..._数学_加菲2日222

编辑： admin           2017-15-06         

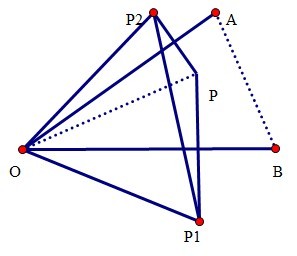
证明： 连接PO

点P1与P关于OB对称,

则 OP1=OP； ∠P1OB=∠POB;

同理：OP2=OP； ∠P2OA=∠POA.

∴ OP1=OP2

∠P1OP2=2∠POA+2∠POB=2（∠POA+∠POB)=60°.

∴ △P1P2O为等边三角形.



其他同学给出的参考思路：

等边三角形。

因为OB垂直平分P1P,所以OP1=OP,同理OP=OP2,所以OP1=OP2,

角P1OB=角BOP，角POA=角AOP2,又因为角BOP+角POA=30，所以角P1OB+角AOP2=30，所以角P1OP2=60,所以三角形P1OP2是等边三角形。

互助这道作业题的同学还参与了下面的作业题

题1： 已知角AOB=30度,点P在角A0B的内部,点P1与P关于OB对称,点P2与P关于OA对称,则P1、O、P2三点的图[数学科目]

构成的三角形是等边三角形.

由题可知：根据中垂线定理得 OP1=OP=OP2,所以△OP1P2是等腰三角形；

又因为：∠AOB=30°,则∠P1PP2=150°,且∠OP1P=∠OPP1,∠OPP2=∠OP2P,故 ∠OP2P+∠OP1P=150°.在四边形OP1PP2中,可得∠P1OP2=60°,以此,等腰三角形OP1P2的顶角为60°,那么这个三角形是等边三角形.

注：图可依据题目画出,便可对答案中的角一目了然.

题2： 已知角AOB=30度,点P在角A0B的内部,点P1与P关于OB对称,点P2与P关于OA对称,则P1、O、P2三点构成什么...已知角AOB=30度,点P在角A0B的内部,点P1与P关于OB对称,点P2与P关于OA对称,则P1、O、P2三点构成什么三[数学科目]

三点构成了等边三角形.

证明;连接OP.

P与P1关于OB对称,则OP1=OP;且∠P1OB=∠POB;

同理:OP2=OP;且∠P2OA=∠POA.

所以:OP1=OP2;且∠P1OP2=2∠POB+2∠POA=2(∠POB+∠POA)=60度.

故:三角形P1P2O为等边三角形.

题3： 【已知∠AOB=45°,点P在∠AOB内部,P1与P关于OB对称P2与P关于OA对称,则P1,O,P2三点构成的三角形是什么我知道是等腰直角三角形步骤(⊙o⊙)?】[数学科目]

△P1OP2是等腰直角三角形

证明：

连接OP

∵P与P1关于OB对称

∴OP=OP1,∠POB=∠P1OB

∵P与P2关于OA对称

∴OP=OP2,∠POB=∠P2OB

∴OP1=OP2=OP

∴△OP1P2是等腰三角形,∠P1OP2=2(∠AOP+∠BOP）=2∠AOB

∵∠AOB=45°

∴∠P1OP2=90°

∴△P1OP2是等腰直角三角形

题4： 【已知角AOB=30°,点P在角AOB的内部,P1与P关于OA对称,P2与P关于OB对称,则角P1PP2＝几度?】[数学科目]

150度

四边形内角和为360度,而又对称可得两个直角,又有一个30度,故所求角为150度

题5： 已知∠AOB=30°，点P在∠AOB内部，点P1与点P关于OA对称，点P2与点P关于OB对称，则△P1OP2是（）A.含30°角的直角三角形B.顶角是30°的等腰三角形C.等边三角形D.等腰直角三角形[数学科目]

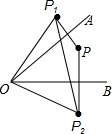∵P为∠AOB内部一点，点P关于OA、OB的对称点分别为P₁、P₂，
∴OP=OP₁=OP₂且∠P₁OP₂=2∠AOB=60°，
∴故△P₁OP₂是等边三角形．
故选C．

•   4
  

相关文章

一公分等于几厘米

一吨等于多少立方米

消费税计算公式

立方米和吨的换算

函数的值域

10公分等于多少厘米

1公斤等于多少千克

数学的由来

一元一次方程计算题

金条多少克