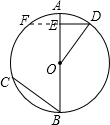
【圆o和圆o上的一点a】如图,已知圆o和圆o上的一点A如果点E在AD弧上,求证;DE..._数学_lfibnzbp
编辑: admin 2017-15-06
-
4
设圆心为O
连接AO,EO、DO
∵AE是正六边形的一边
∴∠AOE=60°
∵AD是正方形一边
∴∠AOD=90°
∴∠EOD=30°
360÷3=12
∴DE是⊙O内接正十二边形的一边.
互助这道作业题的同学还参与了下面的作业题
题1: 如图,已知AB为⊙O的直径,BC=2AD,DE⊥AB,求证:BC=2DE.[数学科目]
 延长DE交圆于点F,根据垂径定理得
延长DE交圆于点F,根据垂径定理得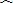 DF=2
DF=2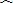 AD
AD
又已知
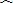 BC=2
BC=2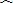 AD,
AD,所以,
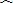 DF=
DF=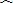 BC,BC=DF,所以BC=2DE.
BC,BC=DF,所以BC=2DE.
题2: 如图,AC是圆O的直径,AB,CD是圆O的两条弦,且弧AD=弧BC,求弧DAB所对的圆周角的大小[数学科目]
结果是90°
因为弧AD=弧BC,所以角BAC=角DAC(等弧所对的圆周角相等)
所以AB‖DC(内错角相等两直线平行)
连接CB,则角DCB即为弧DAB所对的圆周角
因为AC是直径,所以角ABC是90°
所以角DCB=90°(两直线平行,同旁内角互补)
题3: 已知:如图,三角形ABC内接于圆O,D为BS弧的中点,AE垂直BC于E,求证:AD平分角OAE[数学科目]
我也是刚刚做到这道题
其实只要连接OD,OA=OD,所以等腰三角形,两角相等
又D是弧BC中点,根据垂径定理推论,可知OD所在的直径垂直BC,又AE垂直BC于E,有两个直角,所以平行...接下来会了吧~~~~
爬去睡觉.
题4: 【已知,如图,四边形ABCD内接于⊙O,AD是⊙O的直径,BC=CD,∠A=30°,求∠ABC的度数.】[数学科目]
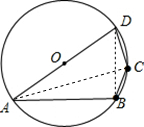 连接AC.
连接AC.
∵AD是圆的直径(已知),
∴∠ACD=90°(直径所对的圆周角是直角),
∵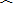 BC
BC
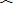 CD(已知),∠A=30°(已知),
CD(已知),∠A=30°(已知),∴∠DAC=∠CAB=12∠A=15°(等弧所对的圆周角相等),
∴∠ADC=75°(直角三角形的两个锐角互为余角);连接BD.
∴∠ADB=60°,
∴∠BDC=∠ADC-∠BDA=75°-60°=15°;
∴在△BCD中,BC=DC,则∠BDC=∠DBC=15°;
∴∠ABC=∠ABD+∠DBC=90°+15°=105°.
题5: 已知:如图,△ABC内接于圆O,AB等于AC,D为弧BC上的任意一点,连接AD,BD.求证:∠ABD=∠AEB好像是要先求∠ABD=∠EAC+∠BCA-这么久了明天早上来看看[数学科目]
是不是AD交BC与点E啊,可能是你没有说大家都不敢回答吧,如果是的话我求采纳最佳啊,闲话少说,开工:
证明:
因为△ABC内接于圆O,且AB等于AC,是A为顶点的等腰三角形
所以∠ABC=∠ACB
又因为∠BAE=∠DAB
所以△ABE∽△ADB (相似定理,或者你用三角形内角和等于180°也行)
所以∠ABD=∠AEB(相似三角形对应角相等)
证明完毕
对于∠ABD=∠EAC+∠BCA,已经证明了∠ABD=∠AEB了,你看下图
∠AEB是△AEC中∠AEC的补角,根据定理三角形其中一个角的补角等于另外两个内角的和,所以∠AEB=∠EAC+∠BCA,即∠ABD=∠EAC+∠BCA,完毕.
最佳吧,
来自数一数二
