【若负三≤x≤2】已知x≤2，求x-3-x+2的最大值与最小值._数学_淡然的草W439

编辑： admin           2017-15-06         

∵当x＜-2时，|x-3|-|x+2|=（3-x）-（-x-2）=3-x+x+2=5；
当-2≤x≤2时，|x-3|-|x+2|=（3-x）-（x+2）=3-x-x-2=1-2x，
∴|x-3|-|x+2|=5，x＜?21?2x，?2≤x≤2

，
∴当x=-2时，|x-3|-|x+2|有最大值：5；
当x=2时，|x-3|-|x+2|有最小值：-3．
∴|x-3|-|x+2|的最大值与最小值分别为：5，-3．

互助这道作业题的同学还参与了下面的作业题

题1： 已知函数f(x)=2sinωx(ω>0)在区间[-π/3,π/4]上的最大值是2,则ω的最小值等于?书上解释说：T/4≤π/4→T≤π.∵T=2π/ω,∴2π/ω≤π→ω≥2.请问T/4≤π/4是怎么得出的?

你可以先画出f(x)=2sinωx的图像

由于它说在区间[-π/3,π/4]上的最大值是2,也就是说对应于最大值的T/4在区间[-π/3,π/4]上,所以

T/4≤π/4



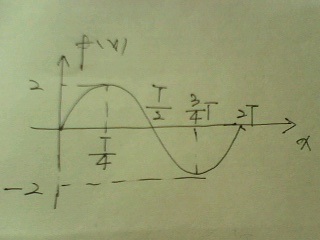
题2： 已知x≥2的最小值是a，x≤-6的最大值是b，则a+b=______．[数学科目]

因为x≥2的最小值是a，a=2；
x≤-6的最大值是b，则b=-6；
则a+b=2-6=-4，
所以a+b=-4．

题3： 已知13≤a≤1，若f（x）=ax2-2x+1在区间[1，3]上的最大值M（a），最小值N（a），设g（a）=M（a）-N（a）．（1）求g（a）的解析式；（2）判断g（a）单调性，求g（a）的最小值．[数学科目]

（1）当13

≤a≤12
时N（a）=f（1a
），M（a）=f（1），
此时g（a）=f（1）-f（1a
）=a+1a
-2；
当12
＜a≤1时N（a）=f（1a
），M（a）=f（3），
此时g（a）=f（3）-f（1a
）=9a+1a
-6；
∴g（a）=a+1a?2 13≤ a≤129a+1a?6 12＜a≤1
…（6分）
（2）当13
≤a≤12
时，∵g（a）=a+1a
-2，∴g′（a）=1-1

a

2
＜0，
∴g（a）在[13
，12
]上单调递减．
同理可知g（a）在（12
，1]上单调递增
∴g（a）_min=g（12
）=12
．…（12分）

题4： 【已知2x-1/3小于等于1＋x-5-3x/2,求|x-1|-|x+3|的最大值和最小值】[数学科目]

(2x-1)/3 -1≥x- (5-3x)/2,两边乘以6得

2(2x-1)-6≥6x-3(5-3x),解得

7/11≥x则|x-1|＝1－x

|x-1|-|x+3|＝1-x-|x+3|

当x大于等于－3小于等于7/11时,|x+3|＝x+3

原式＝1-x-（x+3)＝-2x-4,范围是[-58/11,2]

当x小于－3时候,|x+3|＝-x-3

原式＝1-x-(-x-3)=4.

纵上,最大值是4,最小值是-58/11.

题5： 若0≤x≤2，求函数y=4x-12-3×2x+5的最大值和最小值及相应的x的值．[数学科目]

令t=2^x，∵0≤x≤2
∴1≤t≤4
则y=4

x-12
-3×2^x+5=12
t²-3t+5=12
（t-3）²+12
，1≤t≤4
故当t=3，即x=log₂3时，函数取最小值12
；
当t=1，即x=0时，函数取最大值52
．
•   4
  

相关文章

一公分等于几厘米

一吨等于多少立方米

消费税计算公式

立方米和吨的换算

函数的值域

10公分等于多少厘米

1公斤等于多少千克

数学的由来

一元一次方程计算题

金条多少克