【如图使得a与负1重合】已知：如图1，把矩形纸片ABCD折叠，使得顶点A与边DC上的..._数学_御妹′c11206

编辑： admin           2017-15-06         

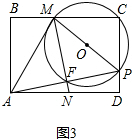
（1）如图：
（2）解法一：AFAN

与APAD
不相等．
假设AFAN＝APAD
，
则由相似三角形的性质，得MN∥DC，
∵∠D=90°
∴DC⊥AD
∴MN⊥AD
∵据题意得，A与P关于MN对称，
∴MN⊥AP
∵据题意，P与D不重合，
∴这与“过一点（A）只能作一条直线与已知直线（MN）垂直”矛盾，
∴假设不成立，
∴AFAN＝APAD
不成立；
解法二：AFAN
与APAD
不相等．
理由如下：
∵P，A关于MN对称，
∴MN垂直平分AP
∴cos∠FAN=AFAN

∵∠D=90°
∴cos∠PAD=ADAP

∵∠FAN=∠PAD
∴AFAN
=ADAP

∵P不与D重合，P在边DC上
∴AD≠AP
∴ADAP
≠APAD

从而AFAN
≠APAD
；
（3）∵AM是⊙O的切线，
∴∠AMP=90°
∴∠CMP+∠AMB=90°
∵∠BAM+∠AMB=90°
∴∠CMP=∠BAM
∵MN垂直平分AP，
∴MA=MP
∵∠B=∠C=90°
∴△ABM≌△MCP
∴MC=AB=4
设PD=x，则CP=4-x
∴BM=PC=4-x
连接HO并延长交BC于J，
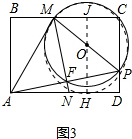
∵AD是⊙O的切线
∴∠JHD=90°
∴HDCJ为矩形
∴OJ∥CP
∴△MOJ∽△MPC
∴OJ：CP=MO：MP=1：2
∴OJ=12
（4-x）
OH=12
MP=4-OJ=12
（4+x）
∵MC²=MP²-CP²
∴（4+x）²-（4-x）²=16
解得：x=1，即PD=1，PC=3
∴BC=BM+MC=PC+AB=3+4=7．
•   4
  

相关文章

一公分等于几厘米

一吨等于多少立方米

消费税计算公式

立方米和吨的换算

函数的值域

10公分等于多少厘米

1公斤等于多少千克

数学的由来

一元一次方程计算题

金条多少克