【直线ab是线段bd】...直线AC平行BD,连结AB,直线AC.BD及线段AB把平面分..._数学_倿雾
编辑: admin 2017-15-06
-
4
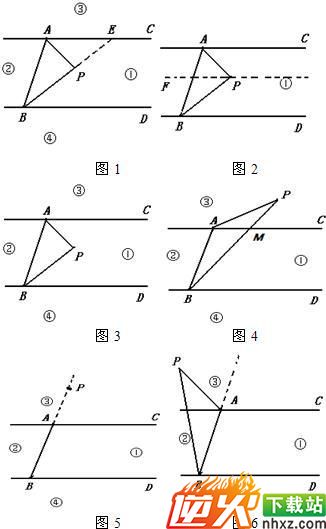
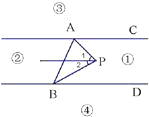
如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
----
分析:(1)如图1延长BP交直线AC于点E,由AC∥BD,可知∠PEA=∠PBD.由∠APB=∠PAE+∠PEA,可知∠APB=∠PAC+∠PBD;
(2)过点P作AC的平行线,根据平行线的性质解答;
(3)根据P的不同位置,分三种情况讨论.
(1)解法一:如图1延长BP交直线AC于点E.
∵AC∥BD,∴∠PEA=∠PBD.
∵∠APB=∠PAE+∠PEA,
∴∠APB=∠PAC+∠PBD;
解法二:如图2
过点P作FP∥AC,
∴∠PAC=∠APF.
∵AC∥BD,∴FP∥BD.
∴∠FPB=∠PBD.
∴∠APB=∠APF+∠FPB
=∠PAC+∠PBD;
解法三:如图3,
∵AC∥BD,
∴∠CAB+∠ABD=180°,
∠PAC+∠PAB+∠PBA+∠PBD=180°.
又∠APB+∠PBA+∠PAB=180°,
∴∠APB=∠PAC+∠PBD.
(2)不成立.
(3)(a)
当动点P在射线BA的右侧时,结论是
∠PBD=∠PAC+∠APB.
(b)当动点P在射线BA上,
结论是∠PBD=∠PAC+∠APB.
或∠PAC=∠PBD+∠APB或∠APB=0°,
∠PAC=∠PBD(任写一个即可).
(c)当动点P在射线BA的左侧时,
结论是∠PAC=∠APB+∠PBD.
选择(a)证明:
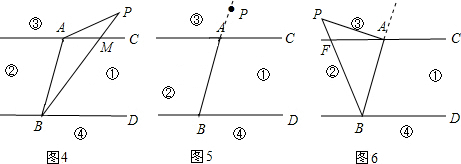
如图4,连接PA,连接PB交AC于M.
∵AC∥BD,
∴∠PMC=∠PBD.
又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠PBD=∠PAC+∠APB.
选择(b)证明:如图5
∵点P在射线BA上,∴∠APB=0度.
∵AC∥BD,∴∠PBD=∠PAC.
∴∠PBD=∠PAC+∠APB
或∠PAC=∠PBD+∠APB
或∠APB=0°,∠PAC=∠PBD.
选择(c)证明:
如图6,连接PA,连接PB交AC于F
∵AC∥BD,∴∠PFA=∠PBD.
∵∠PAC=∠APF+∠PFA,
∴∠PAC=∠APB+∠PBD.
--------
等等图片好不好
其他同学给出的参考思路:
如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
----
分析:(1)如图1延长BP交直线AC于点E,由AC∥BD,可知∠PEA=∠PBD.由∠APB=∠PAE+∠PEA,可知∠APB=∠PAC+∠PBD;
(2)过点P作AC的平行线,根据平行线的性质解答;
(3)根据P的不同位置,分三种情况讨论.
(1)解法一:如图1延长BP交直线AC于点E.
∵AC∥BD,∴∠PEA=∠PBD.
∵∠APB=∠PAE+∠PEA,
∴∠APB=∠PAC+∠PBD;
解法二:如图2
过点P作FP∥AC,
∴∠PAC=∠APF.
∵AC∥BD,∴FP∥BD.
∴∠FPB=∠PBD.
∴∠APB=∠APF+∠FPB
=∠PAC+∠PBD;
解法三:如图3,
∵AC∥BD,
∴∠CAB+∠ABD=180°,
∠PAC+∠PAB+∠PBA+∠PBD=180°.
又∠APB+∠PBA+∠PAB=180°,
∴∠APB=∠PAC+∠PBD.
(2)不成立.
(3)(a)
当动点P在射线BA的右侧时,结论是
∠PBD=∠PAC+∠APB.
(b)当动点P在射线BA上,
结论是∠PBD=∠PAC+∠APB.
或∠PAC=∠PBD+∠APB或∠APB=0°,
∠PAC=∠PBD(任写一个即可).
(c)当动点P在射线BA的左侧时,
结论是∠PAC=∠APB+∠PBD.
选择(a)证明:
如图4,连接PA,连接PB交AC于M.
∵AC∥BD,
∴∠PMC=∠PBD.
又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠PBD=∠PAC+∠APB.
选择(b)证明:如图5
∵点P在射线BA上,∴∠APB=0度.
∵AC∥BD,∴∠PBD=∠PAC.
∴∠PBD=∠PAC+∠APB
或∠PAC=∠PBD+∠APB
或∠APB=0°,∠PAC=∠PBD.
选择(c)证明:
如图6,连接PA,连接PB交AC于F
∵AC∥BD,∴∠PFA=∠PBD.
∵∠PAC=∠APF+∠PFA,
∴∠PAC=∠APB+∠PBD.
--------
等等图片好不好

互助这道作业题的同学还参与了下面的作业题
题1: 【28.如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角.(题示:有】[数学科目]
1、证明:过点P作PE∥AC交AB于E
∵PE∥AC
∴∠PAC=∠APE
∵AC∥BD
∴PE∥BD
∴∠PBD=∠BPE
∵∠APB=∠APE+∠BPE
∴∠APB=∠PAC+∠PBD
2、
∠PAC+∠PBD+∠APB=360
3、
∠PBD-∠PAC=∠APB
题2: 【如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共】[数学科目]
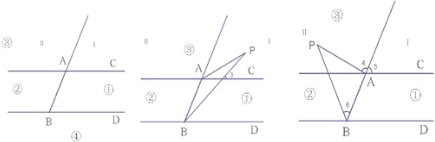
1.过点P作直线AC的平行线(如图),易知∠1=∠PAC,∠2=∠PBD,
又∵∠APB=∠1+∠2,
∴∠APB=∠PAC+∠PBD.
2.不成立.
过点P作AC的平行线PQ,∠APB=∠1+∠2,
∵直线AC∥BD,
∴∠PAC+∠1=180°,∠PBD+∠2=180°,
∴∠PAC+∠1+∠PBD+∠2=360°,
故∠APB=∠PAC+∠PBD不成立.(

3.设射线BA将区域③分成Ⅰ、Ⅱ两部分(如左图),
①若点P位于第Ⅰ部分(如中图),则∠PBD=∠3,∠PAC+∠APB=∠3,
所以∠APB=∠PBD-∠PAC,
②若点P位于第Ⅱ部分(如右图),则∠PBD=∠6+∠ABD,∠PAC=∠4+∠5,∠ABD=∠5,
∴∠PAC-∠PBD=∠4-∠6,
而∠6+∠APB=∠4,
∴∠APB=∠PAC-∠PBD.
③P落在射线BA上时,∠PAC=∠PBD,∠APB=0°.
解析:
1.过点P作AC的平行线,根据平行线的性质将∠PAC,∠PBD等量转化,证出结论.
2.过点P作AC的平行线PQ,∠APB=∠APQ+∠QPB,∠PAC与∠APQ是一对同旁内角,∠QPB与∠PBD也是一对同旁内角,根据两直线平行,同旁内角互补,发现三个角的和是360度.
3.根据BA的延长线上,或两侧分别解答.
题3: 【如图,直线AC平行BD,连接AB,直线AC,BD及线段AB把平面…帮派:龙华帮派号:719596我帮急招人!大家帮帮助!】
如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角) (1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD; (2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立) (3)当动点P在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明. ---- 分析:(1)如图1延长BP交直线AC于点E,由AC∥BD,可知∠PEA=∠PBD.由∠APB=∠PAE+∠PEA,可知∠APB=∠PAC+∠PBD; (2)过点P作AC的平行线,根据平行线的性质解答; (3)根据P的不同位置,分三种情况讨论. (1)解法一:如图1延长BP交直线AC于点E. ∵AC∥BD,∴∠PEA=∠PBD. ∵∠APB=∠PAE+∠PEA, ∴∠APB=∠PAC+∠PBD; 解法二:如图2 过点P作FP∥AC, ∴∠PAC=∠APF. ∵AC∥BD,∴FP∥BD. ∴∠FPB=∠PBD. ∴∠APB=∠APF+∠FPB =∠PAC+∠PBD; 解法三:如图3, ∵AC∥BD, ∴∠CAB+∠ABD=180°, ∠PAC+∠PAB+∠PBA+∠PBD=180°. 又∠APB+∠PBA+∠PAB=180°, ∴∠APB=∠PAC+∠PBD. (2)不成立. (3)(a) 当动点P在射线BA的右侧时,结论是 ∠PBD=∠PAC+∠APB. (b)当动点P在射线BA上, 结论是∠PBD=∠PAC+∠APB. 或∠PAC=∠PBD+∠APB或∠APB=0°, ∠PAC=∠PBD(任写一个即可). (c)当动点P在射线BA的左侧时, 结论是∠PAC=∠APB+∠PBD. 选择(a)证明: 如图4,连接PA,连接PB交AC于M. ∵AC∥BD, ∴∠PMC=∠PBD. 又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和), ∴∠PBD=∠PAC+∠APB. 选择(b)证明:如图5 ∵点P在射线BA上,∴∠APB=0度. ∵AC∥BD,∴∠PBD=∠PAC. ∴∠PBD=∠PAC+∠APB 或∠PAC=∠PBD+∠APB 或∠APB=0°,∠PAC=∠PBD. 选择(c)证明: 如图6,连接PA,连接PB交AC于F ∵AC∥BD,∴∠PFA=∠PBD. ∵∠PAC=∠APF+∠PFA, ∴∠PAC=∠APB+∠PBD.
题4: 如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.[数学科目]
(1)解法一:如图1延长BP交直线AC于点E.
∵AC∥BD,∴∠PEA=∠PBD.
∵∠APB=∠PAE+∠PEA,
∴∠APB=∠PAC+∠PBD;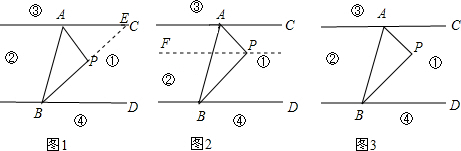
解法二:如图2
过点P作FP∥AC,
∴∠PAC=∠APF.
∵AC∥BD,∴FP∥BD.
∴∠FPB=∠PBD.
∴∠APB=∠APF+∠FPB
=∠PAC+∠PBD;
解法三:如图3,
∵AC∥BD,
∴∠CAB+∠ABD=180°,
∠PAC+∠PAB+∠PBA+∠PBD=180°.
又∠APB+∠PBA+∠PAB=180°,
∴∠APB=∠PAC+∠PBD.
(2)不成立.
(3)(a)
当动点P在射线BA的右侧时,结论是
∠PBD=∠PAC+∠APB.
(b)当动点P在射线BA上,
结论是∠PBD=∠PAC+∠APB.
或∠PAC=∠PBD+∠APB或∠APB=0°,
∠PAC=∠PBD(任写一个即可).
(c)当动点P在射线BA的左侧时,
结论是∠PAC=∠APB+∠PBD.
选择(a)证明:
如图4,连接PA,连接PB交AC于M.
∵AC∥BD,
∴∠PMC=∠PBD.
又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠PBD=∠PAC+∠APB.
选择(b)证明:如图5
∵点P在射线BA上,∴∠APB=0度.
∵AC∥BD,∴∠PBD=∠PAC.
∴∠PBD=∠PAC+∠APB
或∠PAC=∠PBD+∠APB
或∠APB=0°,∠PAC=∠PBD.
选择(c)证明:
如图6,连接PA,连接PB交AC于F
∵AC∥BD,∴∠PFA=∠PBD.
∵∠PAC=∠APF+∠PFA,
∴∠PAC=∠APB+∠PBD.
题5: 【在平面直角坐标系中,如图一,将线段AB平移至线段CD,连接AC、BD.(1)①直接写出图中相等的线段、平行】[数学科目]
AC‖BD,CD‖AB,AC=BD,AB=DC
