【3能分成1加1加1吗】计算1加2分之1加1加2加3分之1一直加到1+2+3+4……n分之1_数学_exKH74QN18
编辑: admin 2017-15-06
-
4
因为1+2+...+n=n(n+1)/2
所以1/(1+2+...+n)=2/[n(n+1)]=2[1/n-1/(n+1)]
所以1/(1+2)+1/(1+2+3)+...+1/(1+2+...+n)
=2[1/2-1/3]+2[1/3-1/4]+...+2[1/n-1/(n+1)]
=2(1/2-1/(n+1))
=(n-1)/(n+1)
其他同学给出的参考思路:
1+2+3+4……n=n(1+n)/2
所以,1/(1+2+3+4……n)=2/[n(1+n)]=2[1/n - 1/(n+1)]
原式=2[1/2+1/2-1/3+……+1/n-1/(n+1)]=2[1-1/(n+1))]=2-2/(n+1)
互助这道作业题的同学还参与了下面的作业题
题1: 计算:负1又3分之1加2又2分之1减3又3分之一加4又2分之1减5又3分之1到加1992又2分之1[数学科目]
负1又3分之1加2又2分之1减3又3分之一加4又2分之1
=(负1又3分之1减3又3分之一)加(2又2分之1加4又2分之1)
=-4又3分之2 +7
=2又3分之1
减5又3分之1到加1992又2分之1
=(1992-5)+(2分之1-3分之1)
=1987+6分之1
=1987又6分之1
题2: 1加2加3一直加到100等于多少简算[数学科目]
(1+100)*50
题3: 1加2分之1加3分之1一直加到n分之1等于多少啊,[数学科目]
要用大学知识解答
调和级数S=1+1/2+1/3+……是发散的
Sn的极限不存在,调和级数发散.
但极限S=lim[1+1/2+1/3+…+1/n-ln(n)](n→∞)却存在
lim Sn(n→∞)≥lim ln(1+1/n)(n→∞)=0
因此Sn有下界
Sn-S(n+1)=1+1/2+1/3+…+1/n-ln(n)-[1+1/2+1/3+…+1/(n+1)-ln(n+1)]
=ln(n+1)-ln(n)-1/(n+1)=ln(1+1/n)-1/(n+1)>ln(1+1/n)-1/n>0
所以Sn单调递减.由单调有界数列极限定理,可知Sn必有极限,因此
S=lim[1+1/2+1/3+…+1/n-ln(n)](n→∞)存在.
lim[1/(n+1)+1/(n+2)+…+1/(n+n)](n→∞)=lim[1+1/2+1/3+…+1/(n+n)-ln(n+n)](n∞)-lim[1+1/2+1/3+…+1/n-ln(n)](n→∞)+lim[ln(n+n)-ln(n)](n→∞)=γ-γ+ln2=ln2
题4: 计算1乘2分之一加2乘三分之一家=加三乘四分之一一直加到n乘(n+1)分之一[数学科目]
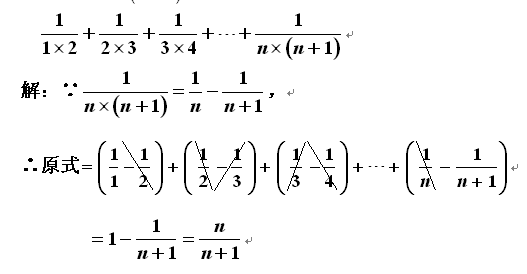
希望有帮助!呵呵!
题5: 【7又5分之2加4又7分之5加2又5分之3,】
很高兴能够在这里回答你的问题,应该为:
7又5分之2加4又7分之5加2又5分之3
=(7又5分之2加2又5分之3)加4又7分之5
=10加4又7分之5
=14又7分之5
