【如图ac垂直bc】如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是..._数学_却雨梅
编辑: admin 2017-15-06
-
4
CE=DF.理由:
在Rt△ABC和Rt△BAD中,AD=BCAB=BA
∴Rt△ABC≌Rt△BAD(HL),
∴AC=BD,∠CAB=∠DBA.
在△ACE和△BDF中,∠CAB=∠DBA∠AEC=∠BFD=90°AC=BD
∴△ACE≌△BDF(AAS),
∴CE=DF.
互助这道作业题的同学还参与了下面的作业题
题1: 如图,AC垂直BC,AD垂直BD,AD=BC,CE垂直AB,DF垂直AB,垂足分别为E、F.求证:CE=DF.图=[数学科目]
∵AC⊥BC,AD⊥BD
∴∠ACB=∠BDA=90°
在Rt△ACB和Rt△BDA中
AB=BA AD=BC
∴Rt△ACB≌Rt△BDA
∴∠ABC=∠BAD
又∵CE⊥AB,DF⊥AB
∴∠AFD=∠BEC=90°
在△ADF和△BCE中
∠BAD=∠CBA ∠AFD=∠BEC AD=BC
∴△ADF≌△BCE
∴CE=DF 别忘了鼓励
题2: 如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是E,F,那么,CE=DF吗?[数学科目]
CE=DF.理由:
在Rt△ABC和Rt△BAD中,AD=BCAB=BA
∴Rt△ABC≌Rt△BAD(HL),
∴AC=BD,∠CAB=∠DBA.
在△ACE和△BDF中,∠CAB=∠DBA∠AEC=∠BFD=90°AC=BD
∴△ACE≌△BDF(AAS),
∴CE=DF.
题3: 如图,已知AC⊥BD,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是E、F.证明:CE=DF[数学科目]
∵AC⊥BC,AD⊥BD
∴∠ACB=∠BDA=90°
在Rt△ACB和Rt△BDA中
AB=BA AD=BC
∴Rt△ACB≌Rt△BDA
∴∠ABC=∠BAD
又∵CE⊥AB,DF⊥AB
∴∠AFD=∠BEC=90°
在△ADF和△BCE中
∠BAD=∠CBA ∠AFD=∠BEC AD=BC
∴△ADF≌△BCE
∴CE=DF
题4: 如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E,F,求证:CE=DF
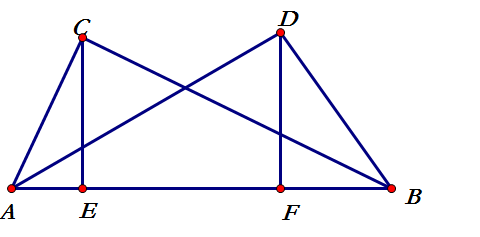
证明:∵AC⊥BC,AD⊥BD,AD=BC
∴Rt△ACB≌Rt△BDA(HL)
∴AC=BD
∠CAB=∠DBA
∵CE⊥AB,DF⊥AB
∴∠CEA=∠DFB=90°
∴△CAE≌△DBF(AAS)
∴CE=DF
记得及时评价啊,希望我们的劳动能被认可,这也是我们继续前进的动力!
题5: 【如图所示,已知AC垂直BC,AD垂直BD,AD=BC,CE垂直AB,DF垂直AB,垂足分别为EF,试证明CE=DF】[数学科目]
∵AC⊥BC,AD⊥BD
∴△ACB和△ADB是直角三角形
∵AD=BC,AB=AB
∴RT△ACB≌RT△ADB(HL)
∴∠CAB=∠DBA即∠CAE=∠DBF
AC=BD
∵CE⊥AB,DF⊥AB
∴∠AEC=∠BFD=90°
∵∠CAE=∠DBF
AC=BD
∴△ACE≌△BDF(AAS)
∴CE=DF
