p为△abc内的一点_浦隙负同学数学作业《p为△abc内的一点》解题方法_数学_浦隙负
编辑: admin 2017-25-06
-
4
p为△abc内的一点导读:
这道数学作业题来自浦隙负同学的作业解题方法分享《p为△abc内的一点》,指导老师是卫老师,涉及到的数学知识点概括为:如图,P为△ABC内任意一点,求证:AB+ACPB+PC.,同学们可以通过学习p为△abc内的一点:如图,P为△ABC内任意一点,求证:AB+ACPB+PC.的相关数学知识来提升自己的数学作业解题能力,只有掌握了这些数学知识能力,才能让自己的数学解题能力提升,也才会在数学考试中取得良好的成绩,下面是浦隙负数学作业的详细总结概括分享(本道题以问答模式展开)。
题目:如图,P为△ABC内任意一点,求证:AB+ACPB+PC.
p为△abc内的一点:逆火学习站的浦隙负同学的作业题:《如图,P为△ABC内任意一点,求证:AB+ACPB+PC.》解题思路
证明:延长BP交AC于点D,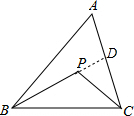
在△ABD中,PB+PD<AB+AD①
在△PCD中,PC<PD+CD②
①+②得PB+PD+PC<AB+AD+PD+CD,
即PB+PC<AB+AC,
即:AB+AC>PB+PC.
互助这道作业题的同学还参与了下面的作业题
题1: 点P是三角形ABC内一点,试说明AB+AC>PB+PC.[数学科目]
延长BP交AC于点E,在△BAE中,AB+AE>BE,即AB+AE>BP+PE ①在△PCE中,CE+PE>PC,②①+②,得,AB+AE+CE+PE>BE+BP+PE即AB+AE+EC>BP+PC所以AB+AC>BP+PCp为△abc内的一点:逆火学习站的浦隙负同学的作业题:《如图,P为△ABC内任意一点,求证:AB+ACPB+PC.》解题思路
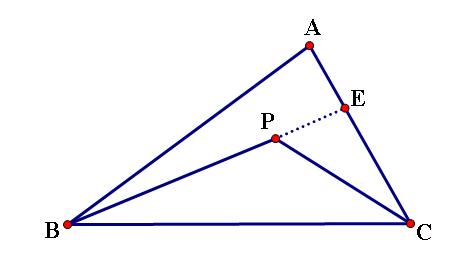
题2: 【P为三角形ABC内任意一点,试说明AB+AC大于PB=PC】[数学科目]
延长BP交AC于点E.在三角形ABE中AB+AE>BE=BP+PE在三角形PEC中PE+EC>PC相加得AB+(AE+EC)+PE>BP+PE+PCAB+AC>BP+CP同理可得BC+AB>AP+CPBC+AC>AP+BPp为△abc内的一点:逆火学习站的浦隙负同学的作业题:《如图,P为△ABC内任意一点,求证:AB+ACPB+PC.》解题思路
再相加两边除以二就可以了!题3: 如图,P为△ABC内任意一点,求证:AB+AC>PB+PC.[数学科目]
证明:延长BP交AC于点D,
在△ABD中,PB+PD<AB+AD①
在△PCD中,PC<PD+CD②
①+②得PB+PD+PC<AB+AD+PD+CD,
即PB+PC<AB+AC,
即:AB+AC>PB+PC.
题4: 如图所示,点p是三角形ABC内一点,判断AB+AC与PB+PC的大小关系,并说明理由.[数学科目]
延长BP与AC交于点Q根据三角形两边和大于第三边三角形ABP,AB+AQ>BQ三角形PQC,QC+PQ>PC相加得AB+AQ+QC+PQ>BQ+PCAB+(AQ+QC)+PQ>(BP+PQ)+PCAB+AC+PQ>BP+PC+PQp为△abc内的一点:逆火学习站(img1.72589.com)的浦隙负同学的作业题:《如图,P为△ABC内任意一点,求证:AB+ACPB+PC.》解题思路
p为△abc内的一点小结:
通过以上关于浦隙负同学对p为△abc内的一点:如图,P为△ABC内任意一点,求证:AB+ACPB+PC.的概括总结详细分享,相信同学们已经对p为△abc内的一点的相关数学作业知识一定有所收获吧。建议同学们要学会归纳总结,仔细揣摩浦隙负同学分享的解答《如图,P为△ABC内任意一点,求证:AB+ACPB+PC.》这道作业题的重点部分,他山之石,可以攻玉,考才获胜。
