圆面积的推导_武反泊同学数学作业《圆面积的推导》解题方法_数学_武反泊
编辑： admin 2017-25-06
-
4
圆面积的推导导读：
这道数学作业题来自武反泊同学的作业解题方法分享《圆面积的推导》，指导老师是鄂老师，涉及到的数学知识点概括为：用积分推导圆面积公式设在直角坐标系上有一圆心在原...，同学们可以通过学习圆面积的推导：用积分推导圆面积公式设在直角坐标系上有一圆心在原...的相关数学知识来提升自己的数学作业解题能力，只有掌握了这些数学知识能力，才能让自己的数学解题能力提升，也才会在数学考试中取得良好的成绩，下面是武反泊数学作业的详细总结概括分享（本道题以问答模式展开）。
题目：用积分推导圆面积公式设在直角坐标系上有一圆心在原...
x^2+y^2=r^2只需算出第一象限,然后乘以4S/4=∫(0到r)√(r^2-x^2)dx令x=rcosa√(r^2-x^2)=rsinadx=-rsinada所以S/4=∫(π/2到0)rsina*(-rsina)da=-r^2∫(π/2到0)(sina)^2da=-r^2∫(π/2到0)(1-cos2a)/2da=-r^2/4∫(π/2到0)(1-cos2a)d2a=-r^2/4(2a-sin2a)(π/2到0)=πr^2/4圆面积的推导：逆火学习站的武反泊同学的作业题：《用积分推导圆面积公式设在直角坐标系上有一圆心在原...》解题思路
所以S=πr^2其他同学给出的参考思路：
把圆n等分 分的数越多 弦长越近似等于弧长 三角形面积越近似等于扇形面积 加起来然后求极限 再积分互助这道作业题的同学还参与了下面的作业题
题1： 圆面积公式推导谁都知道S=圆周率×R^2.但谁会推导?所有书上都找不到.我要严谨的推导,不要想当然的.能用初等数学解决最好.实在不行的话,要用定积分也行,但最好别用参数方程.要严谨详细具[数学科目]
用单位圆说明（r=1）在第一象限中：∫(1-x^2)^(1/2)*dx=∫(1-sint*sint)^(1/2)*d(sint)(t从0到π/2)=∫cost*cost*dt=0.25*∫[1+cos(2t)]*d(2t)=0.25*∫du+0.25*∫cosu*du(u从0到π)=0.25π+0.25*(sinπ-sin0)=0.25π∴在四个象限中：圆面积的推导：逆火学习站的武反泊同学的作业题：《用积分推导圆面积公式设在直角坐标系上有一圆心在原...》解题思路
S=4*0.25π=π题2： 用“因为……所以……”写出圆面积公式的推导过程.小弟感激不尽!鼻涕ing
小学方法：圆面积的推导：逆火学习站的武反泊同学的作业题：《用积分推导圆面积公式设在直角坐标系上有一圆心在原...》解题思路
因为,把一个圆沿半径剪成若干等份,再让一系列圆心角互相咬合,便拼成了一个近似的长方形；而且,平分的份数越多,拼成的与长方形越近似；可以想象,若能无限分割,则就拼成了一个长方形,长相当于圆周长的一半,宽就是圆的半径,所以 S长=a*b=πr*r=πr²圆面积的推导：逆火学习站的武反泊同学的作业题：《用积分推导圆面积公式设在直角坐标系上有一圆心在原...》解题思路
所以S圆=πr²题3： 圆面积的公式怎么推导?除了可以把圆转化成平行四边行或者长方形来推导外,还可以转化成什么图形进行推导?[数学科目]
以圆心为顶点,比如一个圆半径为r,做顶角为w度的n个小三角形,那么每一个三角形面积为r×r×sin(w)÷2.,共有这样的小三角形为360÷w个,所以圆面积r×r×180×sin(w)÷w.从中也可得圆周率为180×sin(w)÷w题4： 写出三角形面积公式的推导过程．（请画图表示，并用文字叙述）[数学科目]
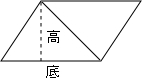如图，将两个完全一样的三角形都可以拼成一个平行四边形，拼成的平行四边形的面积等于这两个三角形的面积，
底等于三角形的底，高等于三角形的高，
所以一个三角形的面积=这个平行四边形的面积的一半，
因为平行四边形的面积=底×高，
三角形的面积×2=底×高，
则三角形的面积=底×高÷2，即S=ah÷2．
题5： 【圆面积的推导公式是什么?星期天我们要展示,可这个推导公式搞晕了,求看得懂的人回复一下.PS：西师版6年及上册P20的议一议.平行四边形面积=二分之一C×r圆面积=1×二分之一πr×r=πr²】[数学科目]
平行四边形面积=底乘高=c×h三角形面积=底乘高的一半=1/2Ch扇形面积=弧长与半径乘积的一半=1/2lr圆面积的推导：逆火学习站(img1.72589.com)的武反泊同学的作业题：《用积分推导圆面积公式设在直角坐标系上有一圆心在原...》解题思路
圆面积的推导小结：
通过以上关于武反泊同学对圆面积的推导：用积分推导圆面积公式设在直角坐标系上有一圆心在原...的概括总结详细分享，相信同学们已经对圆面积的推导的相关数学作业知识一定有所收获吧。建议同学们要学会归纳总结，仔细揣摩武反泊同学分享的解答《用积分推导圆面积公式设在直角坐标系上有一圆心在原...》这道作业题的重点部分，他山之石，可以攻玉，考才获胜。