【函数是直线】【什么是直线方程式】_数学_百马sirP046
编辑: admin 2017-15-06
-
4
形如y=kx+b的方程式称为直线方程式,用文字来表述为:用以表示直线的方程式.它还有许多其它表示方法:
上述写的为斜截式:y=kx+b,知道了斜率和截距的;
点斜式:y-y1=k(x-x1),知道了斜率和过一点(x1,y1)的;
两点式:(y-y1)/(x-x1)=(y2-y1)/(x2-x1),知道了直线过两点(x1,y1),(x2,y2)的;
一般式:Ax+By+C=0.等.
其他同学给出的参考思路:
形如:ax+by+c=0的式子就是直线方程式那么形如y=kx+b的是直线方程式吗? 能不能尽量简单地说明ax+by+c=0具体是什么意思呢? 谢谢了!一般直线方程就是一次函数的形式,由x和y,还有常数构成,当然x,y前还有系数了那么形如ax+by+c=0的式子为什么是直线方程式?...
展开
互助这道作业题的同学还参与了下面的作业题
题1: 【直线方程的一般式与其他几种形式的直线方程相比,它有什么优点】[数学科目]
优点就是它可以表示平面上的任意一条直线,仅此而已.
因为其它式都有特例直线不能表示.比如:
斜截式y=kx+b,就不能表示垂直x轴的直线x=a.
两点式(y-y1)/(y2-y1)=(x-x1)/(x2-x1).不能表示两点x1=x2或y1=y2时的直线(即垂直或水平直线)
截距式x/a+y/b=1不能表示截距为0时的直线,比如正比例直线.
.
但一般式中要确定3个常数a,b,c(虽然其中只有两个是独立的),而其它式只需确定两个常数,所以其它式更简洁一些,实际应用中大多是根据所给的条件,主要选择其它式来做的,为了方便计算.
题2: 直线方程里只有一般式可表示所有方程么?比如斜率不存在的两点式到底行不行……[数学科目]
是的
因为每个式子都有它的局限性
只有一般式适用于任何情况下
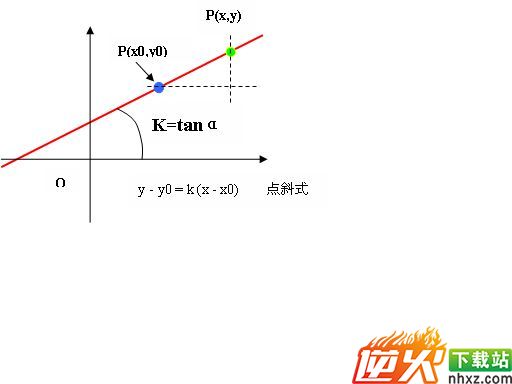
题3: 直线的点斜式方程说的是什么?不太懂,希望能说的详细一些![数学科目]
请看图: 已知一个点:p(x0,y0)和斜率k求直线的方程:
(y-y0)/(x-x0)=k y = y0 + k(x-x0) 此即过点p(x0,y0) 斜率为k的直线方程.
题4: 如何将空间直线的一般式方程化为对称式方程?空间解析几何的知识.比如直线{x+2y-z=7-2x+y+z=7如何化为(x-A)/m=(y-B)/n=(z-C)/p的形式?直线的方向向量是不是方程组中两个平面的法向量的向量积?[数学科目]
对称式由直线上一点和直线的方向向量决定
(1)先求一个交点,将z随便取值解出x和y
不妨令z=0
由x+2y=7
-2x+y=7
解得x=-7/5,y=21/5
所以(-7/5,21/5,0)为直线上一点
(2)求方向向量
因为两已知平面的法向量为(1,2,-1),(-2,1,1)
所求直线的方向向量垂直于2个法向量
由外积可求
方向向量=(1,2,-1)×(-2,1,1)
=
i j k
1 2 -1
-2 1 1
=3i+j+5k
所以直线方向向量为(3,1,5)
因此直线对称式为(x+7/5)/3=(y-21/5)/1=z/5
题5: 【直线的点向式方程和一般式方程如何转换?】[数学科目]
若直线过点P(x0,y0),方向向量v=(v1,v2)
则直线的点向式方程可写为:
v2*(x-x0) - v1*(y-y0)=0
上式去括号得:
v2*x- v2*x0 - v1*y + v1*y0=0
即v2*x - v1*y + v1*y0 - v2*x0 =0
这就是所求的直线的一般式方程,其中法向量n=(v2,-v1)
.
若已知直线的一般式方程为Ax+By+C=0且过点P(x0,y0)
可知直线的法向量n=(A,B)
那么直线的一个方向向量v=(-B,A)
所以直线的点向式方程可写为:A*(x-x0)-(-B)*(y-y0)=0
