【已知BC交DE于O】如图，已知BC，DE相交于点O，给出下面三个论断：①∠B=∠..._数学_噗哧哧5nQ穡
编辑： admin 2017-15-06
-
4
条件：①②
结论：③
已知：∠B=∠E,AB∥DE
求证：BC∥EF
证明：
∵AB∥DE （已知）
∴∠B=∠DOC（两直线平行,同位角相等）
∵∠B=∠E（已知）
∴∠E=∠DOC（等量代换）
∴BC∥EF（同位角相等,两直线平行）
其他同学给出的参考思路：
已知①∠B=∠E；②AB//DE；
求证：③BC//EF
证明：∵AB∥DE
∴∠B＝∠COD
∵∠B=∠E
∴∠COD＝∠E
∴BC∥DE
互助这道作业题的同学还参与了下面的作业题
题1： 【已知如图1：△ABC中，AB=AC，∠B、∠C的平分线相交于点O，过点O作EF∥BC交AB、AC于E、F．②若AB≠AC，其他条件不变，如图2，图中还有等腰三角形吗？如果有，请分别指出它们．另第①问中EF与B】[数学科目]
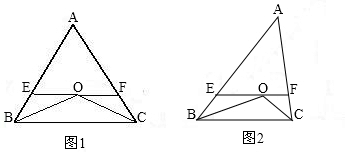（1）有5个等腰三角形，EF与BE、CF间有怎样的关系是：EF=BE+CF=2BE=2CF．理由如下：
∵EF∥BC，
∴∠EOB=∠OBC，∠FOC=∠OCB，
又∠B、∠C的平分线交于O点，
∴∠EBO=∠OBC，∠FCO=∠OCB，
∴∠EOB=∠OBE，∠FCO=∠FOC，
∴OE=BE，OF=CF，
∴EF=OE+OF=BE+CF．
又AB=AC，
∴∠ABC=∠ACB，
∴∠EOB=∠OBE=∠FCO=∠FOC，
∴EF=BE+CF=2BE=2CF；
（2）有2个等腰三角形分别是：等腰△OBE和等腰△OCF；
第一问中的EF与BE，CF的关系是：EF=BE+CF．
（3）有，还是有2个等腰三角形，△EBO，△OCF，EF=BE-CF，理由如下：
∵EO∥BC，
∴∠EOB=∠OBC，∠EOC=∠OCG（G是BC延长线上的一点）
又∵OB，OC分别是∠ABC与∠ACG的角平分线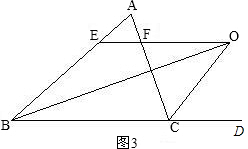
∴∠EBO=∠OBC，∠ACO=∠OCD，
∴∠EOB=∠EBO，
∴BE=OE，
∠FCO=∠FOC，
∴CF=FO，
又∵EO=EF+FO，
∴EF=BE-CF．
题2： 【已知如图1：△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F．①图中有几个等腰三角形?请说明EF与BE、CF间有怎样的关系．②若AB≠AC,其他条件不变,如图2,图中还有等腰三】
（1）有5个等腰三角形,EF与BE、CF间有怎样的关系是：EF=BE+CF=2BE=2CF．理由如下：
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
又∠B、∠C的平分线交于O点,
∴∠EBO=∠OBC,∠FCO=∠OCB,
∴∠EOB=∠OBE,∠FCO=∠FOC,
∴OE=BE,OF=CF,
∴EF=OE+OF=BE+CF．
又AB=AC,
∴∠ABC=∠ACB,
∴∠EOB=∠OBE=∠FCO=∠FOC,
∴EF=BE+CF=2BE=2CF；
（2）有2个等腰三角形分别是：等腰△OBE和等腰△OCF；
第一问中的EF与BE,CF的关系是：EF=BE+CF．
（3）有,还是有2个等腰三角形,△EBO,△OCF,EF=BE-CF,理由如下：
∵EO∥BC,
∴∠EOB=∠OBC,∠EOC=∠OCG（G是BC的BC延长线上的一点）
又∵OB,OC分别是∠ABC与∠ACG的角平分线
∴∠EBO=∠OBC,∠ACO=∠OCG,
∴∠EOB=∠EBO,
∴BE=OE,
∠FCO=∠FOC,
∴CF=FO,
又∵EO=EF+FO,
∴EF=BE-CF．
题3： 已知：如图,AB平行CD,AD交BC于O,EF过点O,分别交AB,CD于点E,F,且AE＝DF.求证：O是EF的中点.[数学科目]
题4： 已知:如图,AB∥CD,AB＝CD,AB与BC交于O点,EF过点O,分别交AB,CD于点E,点F.求证OE＝OF[数学科目]
∵AB∥CD,
∴∠B=∠C
同理：∠A=∠D
∵AB=CD
∴△AOB≌△DOC
∴BO=CO
又∵∠C=∠B
∠COF=∠BOE
∴△COF≌△BOE
∴OE=OF
题5： 如图,点A,B,C,D,E,F都在圆O上,且AB=BC=CD=DE=EF=AF.若⊙O的半径为6,求AE的长[数学科目]
因为 AB=BC=CD=DE=EF=AF,
所以 ABCDEF为正六边形,且弧AF=弧EF,
所以 角AFE=120°
连结OF,AE交AE于P,
因为 弧AF=弧EF,O是圆心
所以 AP=EP,角AFP=角EFP=60°,OF⊥AE,
又因为 AO=6,
所以 AF=OF=AO=6
所以 AP=6/2*根号3=3根号3
所以 AE=6根号3
不知道对不对,将就一下,给我分撒.